Rubriques tendance
#
Bonk Eco continues to show strength amid $USELESS rally
#
Pump.fun to raise $1B token sale, traders speculating on airdrop
#
Boop.Fun leading the way with a new launchpad on Solana.
LLM en tant que juge est devenu un moyen dominant d'évaluer la qualité d'un modèle pour résoudre une tâche, car il fonctionne sans ensemble de test et gère les cas où les réponses ne sont pas uniques.
Mais malgré l'utilisation répandue de cette méthode, presque tous les résultats rapportés sont fortement biaisés.
Je suis ravi de partager notre prépublication sur la manière d'utiliser correctement LLM en tant que juge.
🧵
===
Alors, comment les gens utilisent-ils réellement LLM en tant que juge ?
La plupart des gens utilisent simplement le LLM comme évaluateur et rapportent la probabilité empirique que le LLM indique que la réponse semble correcte.
Lorsque le LLM est parfait, cela fonctionne bien et donne un estimateur non biaisé.
Si le LLM n'est pas parfait, cela ne fonctionne plus.
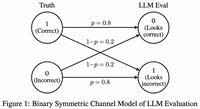
Considérons un cas où le LLM évalue correctement 80 % du temps.
Plus précisément, si la réponse est correcte, le LLM dit "cela semble correct" avec une probabilité de 80 %, et la même probabilité de 80 % s'applique lorsque la réponse est en réalité incorrecte.
Dans cette situation, vous ne devriez pas rapporter la probabilité empirique, car elle est biaisée. Pourquoi ?
Soit p la vraie probabilité que le modèle testé soit correct.
Alors la probabilité empirique que le LLM dise "correct" (= q) est
q = 0.8p + 0.2(1 - p) = 0.2 + 0.6p
Donc l'estimation non biaisée devrait être...


Meilleurs
Classement
Favoris

