トレンドトピック
#
Bonk Eco continues to show strength amid $USELESS rally
#
Pump.fun to raise $1B token sale, traders speculating on airdrop
#
Boop.Fun leading the way with a new launchpad on Solana.
数学的多様体と工学 - フラットアースを通じた説明。
これは簡単に伝えられないし、失敗するかもしれないけど、まあいいや、話してみるよ...
多様体は変わった形で曲がっているものですが、局所的に小さなパッチでは平らな2次元面のように振る舞います。
「フラットアース」という話は、単純な「多様体」問題の良い例です。それは具現化されたエージェントに対して非常に大きな球体であり、エージェントは球体を2次元の平面として解釈しますが、球体自体は...は球面です。
🌎 🌍 🌏
重要な考え方は「局所的に単純、グローバルに複雑」です
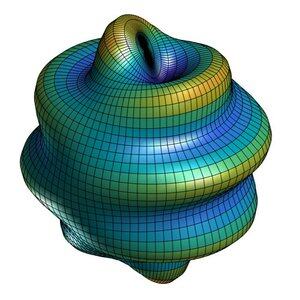
巨大なトーラス世界を考えてみてください。表面上は2次元平面として解釈できますが、全体的には回転軸があり、別の回転軸に巻きつき開口部を形成しています。2次元平面のように無限の体積を均等に分割するのではなく、トーラスは空間を非対称に分割し、内側は有限、外側は無限大です。
局所的には単純、グローバルに複雑です。
工学の多くはこのようなものだ。人間社会の多くはこのような状況です。現実はこういうものです。
ほとんどすべてが多様体であるため、スケールが重要であり、遠近法のスケールも非常に重要です。
しばしば、二人の人間はある問題で強く意見が合わないことがありますが、それは単に視点の尺度が違うだけです。状況は地域ごとに異なり、相手の視点のスケールを認識する心の理論がなければ、そのような意見の相違を橋渡しすることはできません。
このため、組織の階層構造ではEQがIQを支配することが多いのです。
また。。。問題に近づけば近いほど、それを地域で目にする可能性が高くなります。これは一種の「多重罠」と考えてください。非常に優秀な人が集中的に問題に取り組んでも、悪い結果を出すことがあります。
問題は、真の現実である多様体全体を見失うときに起こります。
多くの企業は、エンタープライズソフトウェア、自動車工場、コーヒーショップなど、多様な問題を解決するために存在しています。
...
トップ
ランキング
お気に入り

