Memecahkan Kunci Kurva Elliptic 5-Bit dengan Komputer ⚛️ Kuantum 133-Qubit Eksperimen ini memecahkan kunci kriptografi kurva elips 5-bit menggunakan algoritma Shor. Dieksekusi pada ibm_torino 133-qubit @IBM dengan @qiskit, sirkuit 15-qubit, yang terdiri dari 10 qubit logis dan 5 ancilla, mengganggu Z₃₂ untuk mengekstrak skalar rahasia k dari hubungan kunci publik Q = kP, tanpa pernah mengkodekan k langsung ke dalam oracle. Dari 16.384 bidikan, interferensi kuantum mengungkapkan punggungan diagonal di ruang hasil QFT 32x32. Sirkuit kuantum, lebih dari 67.000 lapisan dalam, menghasilkan pola interferensi yang valid meskipun kedalaman sirkuit ekstrem, dan pasca-pemrosesan klasik mengungkapkan k = 7 dalam 100 hasil teratas yang dapat dibalik (a, b). Panduan Kode 1. Pengkodean Grup Batasi perhatian pada subkelompok ordo-32 ⟨P⟩ kurva elips selama F_p. Petakan titik ke bilangan bulat: 0P -> 0, 1P -> 1, ..., 31P -> 31. Hukum kelompok menjadi penambahan modular: (xP) + (yP) = ((x + y) mod 32))P. Eksperimen ini menggunakan kurva elips selama F_p dengan subkelompok siklik ordo 32, memetakan P -> 1 dan Q = 7P -> 23 di Z₃₂. Kode mengasumsikan perkalian skalar yang telah dihitung sebelumnya, mengabstraksi koordinat eksplisit. 2. Register Kuantum Daftarkan a: lima qubit untuk eksponen a ∈ {0, ..., 31}. Daftar b: lima qubit untuk b ∈ {0, ..., 31}. Daftarkan p: lima qubit yang diinisialisasi ke ∣0⟩ untuk menahan indeks poin. Register klasik c: register 10-bit untuk mencatat nilai terukur a dan b. 3. Persiapan Superposisi Terapkan Hadamard ke setiap qubit dalam a dan b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. U_f konstruksi Oracle Tujuan adalah peta yang dapat dibalik: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Tambahkan aP: untuk setiap bit a_i (berat 2^i), tambahkan (2^i P) mod 32 Tambahkan bQ: komputasi (2^i Q) mod 32, lalu tambahkan dikontrol pada b_i. Ini menggunakan gerbang permutasi terkontrol 5-qubit. Semua konstanta berasal dari generator kurva elips P dan titik publik Q. Tidak ada gerbang yang pernah secara langsung merujuk pada rahasia k. 5. Keadaan Global setelah Oracle Negara berkembang menjadi: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, di mana f(a, b) = a + kb (mod32). a, b 6. Daftar Titik Isolasi Algoritma hanya membutuhkan hubungan fase dalam a, b. Penghalang mengisolasi p. 7. Transformasi Fourier Kuantum (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Pola Interferensi Amplitudo sendi untuk mengamati (u, v) adalah: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), yang membentuk punggungan diagonal di kisi hasil 32x32. 9. Pengukuran Ukur kesepuluh qubit logis. Hasil berkonsentrasi pada 32 pasangan berbeda yang memuaskan u + kv ≡ 0 (mod 32). 10. Pasca-Pemrosesan Klasik Bitstring dibalik endian dan diurai menjadi (a, b) pasangan. Simpan hanya baris di mana gcd(b, 32) = 1, memastikan b tidak dapat dibalikkan. Kunci kandidat dihitung sebagai: k = (-a) b^(-1) mod 32 Naskahnya kemudian: Mengekstrak 100 hasil teratas yang dapat dibalik (a, b) dengan jumlah tertinggi. Menghitung k untuk masing-masing. Mencetak setiap (a, b) pasangan, k yang dipulihkan, dan hitungan. Menyatakan keberhasilan jika k = 7 muncul di 100 teratas. 11. Verifikasi dan Penyimpanan Skalar yang benar k = 7 dikonfirmasi jika muncul di 100 hasil teratas yang dapat dibalik. Semua jumlah bitstring mentah, tata letak qubit, dan metadata disimpan ke JSON untuk visualisasi dan analisis lebih lanjut. Hasil 2025-06-25 19:41:29,294 | INFORMASI | Kedalaman sirkuit 67428, jumlah gerbang OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Mengirimkan pekerjaan menggunakan opsi {'options': {}, 'version': 2, 'support_qiskit': True} SUKSES — k = 7 ditemukan di hasil 100 teratas 100 pasangan terbalik (a, b) teratas dan k yang dipulihkan: (a= 8, b=11) → k = 8 (hitungan = 63) (a=12, b= 9) → k = 20 (hitungan = 58) (a = 0, b = 3) → k = 0 (hitungan = 54) (a= 1, b= 9) → k = 7 (hitungan = 54) <<< (a=28, b= 1) → k = 4 (hitungan = 53) (a = 0, b = 11) → k = 0 (hitungan = 53) (a= 8, b= 9) → k = 24 (hitungan = 53) (a= 8, b= 3) → k = 8 (hitungan = 53) ... (a=11, b= 3) → k = 7 (hitungan = 41) <<< ... (a=25, b= 1) → k = 7 (hitungan = 32) <<< Eksekusi ini berhasil mengambil skalar rahasia k = 7 menggunakan kunci ECC 5-bit (subgrup urutan-32), memperluas serangan 4-bit saya sebelumnya ke ruang dengan 1024 kemungkinan kombinasi (a, b) dan φ(32) = 16 nilai b yang dapat dibalik. k = 7 muncul tiga kali di 100 teratas: (a = 1, b = 9) -> k = 7 dengan 54 hitungan (a = 11, b = 3) -> k = 7 dengan 41 hitungan (a = 25, b = 1) -> k = 7 dengan 32 hitungan Ini adalah keadaan frekuensi tinggi, menjadikannya vektor serangan yang kredibel di bawah pasca-pemrosesan klasik. Hitungan menunjukkan konsentrasi di sekitar hubungan modular terstruktur: a + kb ≡ 0 mod 32. Ini muncul sebagai punggungan diagonal di ruang pengukuran 32x32. Beberapa nilai k sering berulang (k = 0, 24, 28), menunjukkan tumpang tindih probabilistik intrinsik terhadap interferensi kuantum, beberapa di antaranya adalah positif palsu dari noise atau aliasing dengan kesetaraan modular lainnya. Kedalaman sirkuit adalah 67.428, dengan total 106.455 gerbang, mencerminkan rutinitas kuantum yang besar dan kompleks untuk aritmatika indeks modular terkontrol. Ini mungkin jumlah gerbang terbesar yang pernah saya gunakan di sirkuit. Jumlah gerbang untuk sirkuit: Nomor Telepon: 56613 CZ: 34319 RZ: 15355 x: 157 ukuran: 10 penghalang: 1 Total gerbang: 106455 Tebal: 67428 Lebar: 133 qubit | 10 clbit Eksperimen ini membutuhkan waktu 54 detik untuk diselesaikan pada 'ibm_torino'. Profil kebisingan tidak seragam tetapi membusuk, yang berarti sistem kuantum kemungkinan menyelesaikan harmonik dominan dalam interferensi tetapi mengaburkan struktur yang lebih halus. Ekor distribusi masih berisi k = 7 kandidat yang valid, ini mendukung serangan kuantum gaya kamus di mana pemindaian hasil top-N (N = 100) cukup untuk mengambil kunci. 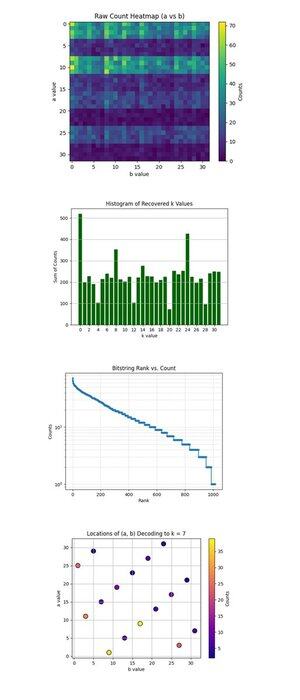Peta Panas Hitungan Mentah (a vs b) di atas (kode lengkap di Qwork) menunjukkan kisi 32x32 mewakili hitungan yang diamati untuk setiap pasangan (a, b) setelah menjalankan sirkuit Shor. Peta panas menunjukkan distribusi berpita dan tidak merata, menunjukkan tonjolan gangguan, bukan kebisingan. Baris tertentu (nilai a) memiliki konsentrasi yang terlihat lebih tinggi, menunjukkan interferensi konstruktif di sepanjang solusi a + kb ≡ 0 mod 32 tertentu. Histogram Nilai k yang Dipulihkan di atas (kode lengkap pada Qwork) mengumpulkan jumlah total untuk setiap kunci skalar yang dipulihkan k ∈ Z₃₂, yang diturunkan melalui k = −ab^(−1) mod 32. Lonjakan besar pada k = 0 dan satu lagi di sekitar k = 24 dominan. Kunci yang benar k = 7 bukanlah yang tertinggi, tetapi terwakili dengan baik (~54 + 41 + 32 = 127 hitungan di beberapa pasangan (a, b). Ini menunjukkan bahwa peretas dapat menyerang kamus hasil dalam jumlah yang lebih besar. Bitstring Rank vs Count (Log-Scale) di atas (kode lengkap di Qwork) menunjukkan plot peringkat seperti Zipf dari semua bitstring dengan jumlah menurun. Sumbu y skala log menunjukkan ekor eksponensial, sebagian besar hasil terjadi <10 kali. Bitstring kepala (atas ~50) memiliki probabilitas yang jauh lebih tinggi, menunjukkan puncak interferensi konstruktif. Anda dapat membangun serangan kamus heuristik kuantum yang hanya memanen N bitstring teratas dengan pengembalian sinyal eksponensial. Ini memvalidasi struktur sinyal-ke-kebisingan kuantum masih utuh bahkan dengan sirkuit yang lebih panjang (kedalaman 67428). Lokasi (a, b) Decoding ke k = 7 di atas (kode penuh pada Qwork) menunjukkan setiap titik adalah pasangan (a, b) yang didekodekan menjadi k = 7. Intensitas warna sama dengan berapa kali pasangan ini terjadi. Plot menunjukkan distribusi yang relatif seragam di (a, b), tetapi dengan puncak lokal di (1, 9), (11, 3), (25, 1). Beberapa kombinasi (a, b) menyatu menjadi k = 7 dengan multiplisitas yang tidak seragam. Dari sudut pandang kriptoanalitik, ini memvalidasi bahwa algoritme Shor dapat dengan andal memecahkan kunci ECC bahkan ketika k yang benar bukan hasil 1 teratas. Inversibilitas Mask untuk b Register di atas (kode lengkap di Qwork) menunjukkan bagan batang hitungan untuk setiap b ∈ {0, ..., 31} yang merupakan coprime dengan 32 (gcd(b, 32) = 1, hanya ini modulo 32 yang dapat dibalik dan berguna untuk memulihkan k melalui: k = (−a)b^(−1) mod 32. B yang dapat dibalik dihuni dengan baik, menunjukkan sirkuit memang menghasilkan kandidat yang dapat dipulihkan. Lebih banyak keseragaman di sini akan meningkatkan daya pasca-pemrosesan, idealnya, ini akan datar. Peta Frekuensi Terbalik Modular: b vs b^(−1) mod 32 di atas (kode lengkap di Qwork) menunjukkan peta panas seberapa sering setiap b yang dapat dibalik memetakan ke setiap modular terbalik b^(−1) mod 32 yang sesuai, ditimbang dengan jumlah hasil. Sebagian besar titik jatuh pada garis bijektif yang bersih, masing-masing b dipetakan dengan bersih ke b^(−1) yang unik, mengkonfirmasi kebenaran inversi modular. Wilayah yang lebih terang (dekat kiri bawah atau kanan atas) menunjukkan b yang disukai dari pengambilan sampel kuantum. Tidak ada kebisingan atau pengelompokan off-diagonal, pertanda baik dari struktur modular yang bersih dipertahankan. Peta a + 7b mod 32 di atas (kode lengkap di Qwork) mengasumsikan k = 7 dan memplot nilai (a + 7b) mod 32 di semua hasil. Distribusinya hampir seragam. Ini menunjukkan tidak ada punggungan interferensi tajam seperti pada casing 4-bit. Mengapa? Sirkuit 5-bit (dengan 10 qubit logis) menyebarkan amplitudo lebih tipis di 1024 hasil, mengurangi kontras. Namun kunci yang benar masih dapat dipulihkan, menunjukkan banyak jalan yang lemah konstruktif, daripada beberapa yang dominan. Efisiensi Serangan ECC: Valid vs Tidak Valid b di atas (kode lengkap di Qwork) menunjukkan jumlah total dari sampel dengan b yang dapat dibalik (berguna untuk pemulihan kunci) vs. b yang tidak dapat dibalik (tidak berguna). Lebih dari setengah hasil terbuang-pada nilai b yang tidak valid (gcd(b, 32) != 1). Desain berikutnya untuk jeda 6 bit dapat menggunakan masking oracle atau pemfilteran pascaseleksi pada domain b yang valid. 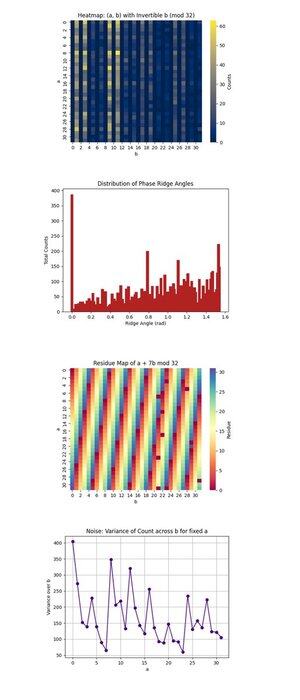Peta Panas: (a, b) dengan Inreversible b (mod 32) di atas (kode lengkap di Qwork) hanya berfokus pada pasangan (a, b) di mana b adalah modulo 32 yang dapat dibalik, kondisi yang diperlukan untuk memulihkan k. Ini menunjukkan di mana interferensi kuantum terkonsentrasi dalam ruang 1024 titik. Daerah intensitas tinggi mengungkapkan jalur interferensi yang disukai, menunjukkan keadaan kuantum berevolusi secara tidak seragam, mungkin mendukung orbit tertentu di bawah perkalian modular. Ini menegaskan koherensi sinyal yang cukup kuat di beberapa wilayah untuk mengisolasi kandidat yang valid. Distribusi Sudut Punggungan Fase di atas (kode lengkap pada Qwork) membincangkan sudut yang dibentuk oleh vektor (-a, b) dalam bidang, modulo π, yang kira-kira sesuai dengan tonjolan fase dalam ruang QFT. Puncak dalam histogram menunjukkan keselarasan yang kuat, resonansi, dari bentuk u + kv ≡ 0, yang berarti rangkaian berhasil mengkodekan k ke dalam pola interferensi meskipun ruang keadaan penuh sangat luas. Beberapa sudut dominan menunjukkan harmonisk pergeseran tersembunyi hadir. Peta Residu dari a + 7b mod 32 di atas (kode lengkap di Qwork) memvisualisasikan residu keluaran untuk kunci target tertentu k = 7, di seluruh ruang (a, b). Setiap pita atau simetri yang konsisten di sini menunjukkan seberapa baik interferensi memperkuat solusi yang valid (di mana nilai ini sama dengan 0). Anda dapat mengamati wilayah mana dari kisi 1024 yang sesuai dengan + 7b ≡ 0, memvalidasi bahwa struktur oracle mengarah pada pencetakan kunci yang berhasil. Kebisingan: Varians Hitungan di b untuk fixed a di atas (kode lengkap pada Qwork) menunjukkan seberapa bising atau stabil jumlah output untuk setiap fixed a saat kita memvariasikan b. Varians tinggi berarti beberapa nilai b mengarah pada amplifikasi yang kuat sementara yang lain tidak, menyiratkan sensitivitas sirkuit atau kebisingan backend untuk baris a tersebut. Daerah halus menyiratkan koherensi kuantum, sedangkan lonjakan dapat menunjukkan dekoherensi atau propagasi kesalahan selama evaluasi oracle. Pada akhirnya, eksperimen ini berhasil memecahkan kunci kurva elips 5-bit menggunakan algoritma Shor yang dijalankan pada prosesor kuantum 133-qubit IBM, memperluas hasil 4-bit sebelumnya ke ruang interferensi yang jauh lebih besar (32x32 = 1024 hasil). Sirkuit ini mengkodekan oracle di atas Z₃₂ tanpa pernah merujuk pada skalar rahasia k, dan memanfaatkan aritmatika kelompok modular untuk menjerat skalar ke dalam interferensi fase. Sirkuit kuantum, lebih dari 67.000 lapisan dalam, menghasilkan pola interferensi yang valid meskipun kedalaman sirkuit ekstrem, dan pasca-pemrosesan klasik mengungkapkan k = 7 dalam 100 hasil teratas yang dapat dibalik (a, b). Melalui visualisasi eksperimen ini mengkonfirmasi struktur punggungan diagonal, topeng inversibilitas, dan penyelarasan harmonik punggungan interferensi, memvalidasi bahwa koherensi kuantum tetap cukup kuat untuk memperkuat hubungan modular yang benar. Ini menetapkan bahwa algoritma Shor terus menskalakan di bawah rezim sirkuit yang lebih dalam dan bahwa strategi pemulihan kunci berbasis kamus (pencacahan 100 teratas) tetap layak saat panjang bit meningkat, menunjukkan keuntungan kuantum yang jelas bahkan dalam kondisi dunia nyata yang bising. Kode # Sirkuit utama # Impor Pencatatan impor, JSON Dari GCD Impor Matematika Impor Numpy sebagai NP dari qiskit impor QuantumCircuit, QuantumRegister, ClassicalRegister, transpile dari qiskit.circuit.library impor UnitaryGate, QFT dari qiskit_ibm_runtime impor QiskitRuntimeService, SamplerV2 Impor panda sebagai PD # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANS = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Pengguna/steventippeconnic/Unduhan/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" TEMBAKAN = 16384 # Parameter kurva mainan (subkelompok ordo-32 dari E(F_p)) URUTAN = 32 # |E(F_p)| = 32 P_IDX = 1 # Genset P -> indeks 1 Q_IDX = 23 # Titik publik Q = kP, di sini "23 mod 32" untuk k = 7 # Pembantu pencatatan logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(nama tingkat)s | %(pesan)s") log = logging.getLogger(__name__) # Pilihan qubit berbasis kalibrasi def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() pemenang = ( df.sort_values(["kesalahan √x (sx)", "T1 (kami)", "T2 (kami)"], ascending=[Benar, Salah, Salah]) ["Qubit"].head(n).tolist() ) log .info("Qubit fisik terbaik: %s", pemenang) kembali pemenang N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, titik FISIK = best_qubits(CAL_CSV, N_Q_TOTAL) # Modulo adder konstan 32 sebagai gerbang yang dapat digunakan kembali def add_const_mod32_gate(c: int) -> UnitaryGate: """Kembalikan gerbang 5-qubit yang memetakan |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.nol((32, 32)) untuk x dalam jangkauan(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) untuk c dalam rentang(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, konstan): """Terapkan |x⟩ → |x+konstanta (mod 32)⟩ dikendalikan oleh satu qubit.""" qc.append(ADDERS[konstan].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (mod aritmatika indeks 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): untuk i dalam rentang (N_Q): konstanta = (P_IDX * (1 << i)) % URUTAN Jika konstan: controlled_add(qc, a_reg[i], point_reg, konstanta) untuk i dalam rentang (N_Q): konstanta = (Q_IDX * (1 << i)) % ORDER jika konstanta: controlled_add(qc, b_reg[i], point_reg, konstanta) # Bangun sirkuit Shor penuh def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.penghalang() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=Salah), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) Kembali QC # Eksekusi IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANS) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=FISIK, optimization_level=3) log .info("Kedalaman sirkuit %d, jumlah gerbang %s", trans.depth(), trans.count_ops()) sampler = SamplerV2 (mode = backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Pasca-pemrosesan klasik creg_name = trans.cregs[0].name counts_raw = hasil[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): mengembalikan int(bs[::-1], 2) hitungan = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v untuk k, v dalam counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Kriteria keberhasilan. Periksa 100 baris terbalik teratas untuk k = 7 top_invertibles = [] Untuk (a_val, b_val), freq di atas: jika gcd(b_val, ORDER) != 1: terus inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % PESANAN top_invertibles.append(((a_val, b_val), k_candidate, freq)) jika len(top_invertibles) == 100: pecah # Periksa keberhasilan dan cetak hasil found_k7 = any(k == 7 untuk (_, k, _) dalam top_invertibles) Jika found_k7: print("\nSUKSES — k = 7 ditemukan di 100 hasil teratas\n") lain: print("\nPERINGATAN — k = 7 TIDAK ditemukan di 100 hasil teratas\n") print("100 pasangan terbalik (a, b) teratas dan k yang dipulihkan:") untuk (a, b), k, hitung dalam top_invertibles: tag = " <<<" jika k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (hitungan = {hitung}){tag}") # Simpan data mentah keluar = { "eksperimen": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": FISIK, "tembakan": TEMBAKAN, "Hitungan": counts_raw } JSON_PATH = "/Pengguna/steventippeconnic/Dokumen/QC/Shors_ECC_5_Bit_Key_0.json" dengan open(JSON_PATH, "w") sebagai fp: json.dump(keluar, fp, indentasi=4) log .info("Hasil disimpan → %s", JSON_PATH) # Akhir Kode lengkap untuk semua visualisasi menggunakan data eksekusi di Qwork.