133量子ビット量子コンピューター⚛️による5ビット楕円曲線キーの解読 この実験では、ショアのアルゴリズムを使用して5ビットの楕円曲線暗号鍵を解読します。@IBMの133量子ビットibm_torinoと@qiskitで実行される15量子ビット回路は、10個の論理量子ビットと5個の補助量子ビットで構成され、Z₃₂に干渉して公開鍵の関係Q = kPから秘密のスカラーkを抽出します。16,384 回のショットから、量子干渉により、32x32 QFT 結果空間の斜めの隆起が明らかになりました。67,000層以上の深さの量子回路は、極端な回路深度にもかかわらず有効な干渉パターンを生成し、古典的な後処理では、上位100の可逆性(a、b)結果でk = 7が明らかになりました。 コードのチュートリアル 1. グループエンコーディング F_p上の楕円曲線の次数32サブグループ⟨P⟩に注意を限定します。 ポイントを整数にマップします。 0P -> 0、1P -> 1、...、31P -> 31。 群法はモジュラー加算になります。 (xP) + (yP) = ((x + y) mod 32))P. この実験では、次数 32 の周期サブグループを持つ F_p 上の楕円曲線を使用し、Z ₃₂ で P -> 1 と Q = 7P -> 23 をマッピングします。このコードでは、事前計算されたスカラー乗算を前提としており、明示的な座標を抽象化しています。 2. クォンタムレジスタ レジスタ a: 指数 a ∈ {0, ..., 31} の 5 量子ビット。 レジスタ b: b ∈ {0, ..., 31} の 5 量子ビット。 レジスタ p: ポイント インデックスを保持するために ∣0⟩ に初期化された 5 つの量子ビット。 クラシックレジスタc:aとbの測定値を記録するための10ビットレジスタ。 3. 重ね合わせの準備 a と b のすべての量子ビットにアダマールを適用します。 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. オラクル構築U_f Goalはリバーシブルマップです。 ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. aPを追加:各ビットa_i(重み2 ^ i)に対して、(2 ^ i P)mod 32を追加します bQを追加します:計算(2 ^ i Q)mod 32、次にb_iで制御を追加します。 これらは、5量子ビット制御の順列ゲートを使用します。すべての定数は、楕円曲線のジェネレータ P と公開点 Q から導出されます。 どのゲートも直接シークレットkを参照することはありません。 5. オラクル後のグローバルステート 状態は次のように進化します。 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩、ここでf(a, b) = a + kb (mod32). a、b 6. アイソレート・ポイント・レジスタ アルゴリズムに必要なのは、a、b の位相関係だけです。障壁はpを分離します。 7. 量子フーリエ変換(QFT) QFTの31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u = 0 QFTの31 (2)b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. 干渉パターン 観測の同時振幅(u、v)は次のとおりです。 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(U + kV ≡ 0 (mod 32)) で、32x32 結果グリッドに対角線上の隆起を形成します。 9. 測定 10 個の論理量子ビットをすべて測定します。結果は、u + kv ≡ 0 を満たす 32 の異なるペアに集中します (mod 32)。 10. 従来のポストプロセッシング ビット文字列はエンディアン反転され、(a, b) ペアに解析されます。gcd(b, 32) = 1 の行のみを保持し、b が可逆であることを確認します。候補キーは次のように計算されます。 k = (-a) b^(-1) mod 32 スクリプトは、次の操作を行います。 上位 100 件の最もカウントの高い可逆性 (a, b) の結果を抽出します。 それぞれについてkを計算します。 各(a、b)ペア、回復されたk、およびカウントを印刷します。 k = 7 がトップ 100 に登場した場合、成功を宣言します。 11. 検証と保管 正しいスカラー k = 7 は、上位 100 の可逆結果に現れる場合、確認されます。 すべての生のビット文字列カウント、量子ビット レイアウト、メタデータは JSON に保存され、さらに視覚化と分析が行われます。 業績 2025年6月25日 19:41:29,294 |お知らせ |回路の深さ 67428、ゲート数 OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: オプションを使用してジョブを送信しています {'options': {}, 'version': 2, 'support_qiskit': True} SUCCESS — 上位 100 件の結果で k = 7 が見つかりました 上位 100 個の可逆 (a, b) ペアと回復した k: (a = 8、b = 11) → k = 8 (カウント = 63) (a = 12、b = 9) → k = 20 (カウント = 58) (a = 0、b = 3) → k = 0 (カウント = 54) (a = 1、b = 9) → k = 7 (カウント = 54) <<< (a = 28、b = 1) → k = 4 (カウント = 53) (a = 0、b = 11) → k = 0 (カウント = 53) (a = 8、b = 9) → k = 24 (カウント = 53) (a = 8、b = 3) → k = 8 (カウント = 53) ... (a = 11、b = 3) → k = 7 (カウント = 41) <<< ... (a=25, b= 1) → k = 7 (count = 32) <<< この実行では、5 ビット ECC キー (order-32 サブグループ) を使用して秘密のスカラー k = 7 を正常に取得し、前の 4 ビット攻撃を 1024 の可能な (a, b) の組み合わせと φ(32) = 16 の可逆 b 値を持つ空間に拡張します。k = 7 は、上位 100 に 3 回表示されます。(a = 1, b = 9) -> k = 7 で 54 カウントです (a = 11、b = 3) -> k = 7、41カウント (a =25、b = 1) -> k = 7、32カウント これらは高頻度の状態であるため、従来のポストプロセッシングでは信頼できる攻撃ベクトルとなります。 カウントは、構造化されたモジュラー関係 (a + kb ≡ 0 mod 32) の周りの集中を示しています。これらは、32x32 の測定空間に対角線上の隆起として表示されます。いくつかのk値が頻繁に繰り返され(k = 0、24、28)、量子干渉に固有の確率的オーバーラップを示しており、これらの一部はノイズや他のモジュラー等価性とのエイリアシングによる誤検知です。 回路の深さは67,428で、合計106,455ゲートであり、制御されたモジュラーインデックス演算の大規模で複雑な量子ルーチンを反映しています。これは、私が回路で使用したゲートの中で最も多い量かもしれません。 回路のゲート数: SXの:56613 CZの34319 RZ:15355 X:157 メジャー:10 バリア:1 ゲート総数:106455 奥行き: 67428 幅: 133 量子ビット | 10 CLBITの この実験は「ibm_torino」で完了するまでに54秒かかりました。 ノイズプロファイルは不均一ですが減衰しているため、量子システムは干渉の支配的な高調波を解き明かした可能性がありますが、より細かい構造はぼやけています。ディストリビューションの裾にはまだ有効なk = 7の候補が含まれており、これは、上位N個の結果スキャン(N = 100)でキーを取得するのに十分な辞書スタイルの量子攻撃をサポートします。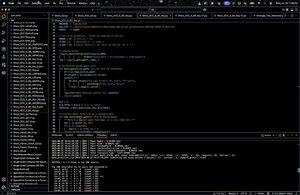 上記の Raw Count ヒートマップ (a vs b) (Qwork のフルコード) は、32x32 グリッドが Shor の回路を実行した後に各ペア (a, b) で観測されたカウントを表していることを示しています。ヒートマップは、ノイズではなく干渉リッジを示す、縞模様で不均一な分布を示しています。特定の行 (a 値) は目に見えて高い濃度を示しており、特定の a + kb ≡ 0 mod 32 溶液に沿った建設的な干渉を示唆しています。 上記の復元された k 値のヒストグラム (Qwork のフルコード) は、復元された各スカラー キー k ∈ Z₃₂ の合計カウントを集計し、k = −ab^(-1) mod 32 によって導き出されます。k = 0 での大きなスパイクと k = 24 付近の別のスパイクが支配的です。正しいキー k = 7 は最高ではありませんが、適切に表現されています (~54 + 41 + 32 = 127 は複数の (a, b) ペアでカウントされます)。これは、ハッカーが大量の結果を辞書攻撃できることを示しています。 上記のビット文字列ランク対カウント(対数スケール)(Qworkのフルコード)は、すべてのビット文字列の降順カウントによるZipfのようなランクプロットを示しています。対数スケールのy軸は指数関数的な裾を示し、ほとんどの結果は<10回発生します。ヘッド (上位 ~50) ビットストリングの確率は急激に高く、建設的な干渉ピークを示しています。上位 N ビット文字列のみを収集し、信号の指数関数的リターンを持つ量子ヒューリスティック辞書攻撃を構築できます。これは、量子信号対雑音構造が長い回路(深さ67428)でも損なわれていないことを検証しています。 上記の (a, b) の k = 7 へのデコード (Qwork のフルコード) の位置は、各ドットが k = 7 にデコードされた (a, b) ペアであることを示しています。色の濃さは、このペアが発生した回数と等しくなります。 プロットは、(a, b) 全体で比較的均一な分布を示していますが、(1, 9)、(11, 3)、(25, 1) に局所的なピークがあります。複数の (a, b) の組み合わせは、不均一な多重度で k = 7 に収束します。暗号解析の観点からは、これは、正しいkが上位1の結果でない場合でも、ShorのアルゴリズムがECCキーを確実に解読できることを検証しています。 上記の b レジスタの可逆性マスク (Qwork のフル コード) は、32 (gcd(b, 32) = 1、これらのみが可逆モジュロ 32 であり、次のようにして k を回復するのに役立つ各 b ∈ {0, ..., 31} のカウントの棒グラフを示しています。 k = (−a)b^(−1) mod 32.可逆 b は十分に配置されており、回路が回復可能な候補を生成したことを示しています。ここでの均一性を高めると、後処理能力が向上し、理想的には、これらはフラットになります。 上記のモジュラー逆周波数マップ: b vs b^(-1) mod 32 (Qwork のフルコード) は、各可逆 b が対応する各モジュラー逆 b^(-1) mod 32 にマップされる頻度のヒートマップを、結果カウントで重み付けしたものです。ほとんどの点はきれいな全単射線上にあり、各 b は一意の b^(−1) にきれいに写像され、モジュラー反転の正確さが確認されます。明るい領域 (左下または右上付近) は、量子サンプリングから好まれる b を示しています。対角線を外れたノイズやクラスタリングはなく、クリーンなモジュラー構造が維持されています。 上記の a + 7b mod 32 マップ (Qwork のフル コード) は、k = 7 と仮定し、すべての結果で (a + 7b) mod 32 の値をプロットしています。分布はほぼ均一です。これは、4ビットの場合のような鋭い干渉リッジがないことを示唆しています。なぜでしょうか。5ビット回路(10個の論理量子ビットを使用)は、1024の結果にわたって振幅を薄く広げ、コントラストを低下させます。それでも、正しいキーはまだ回復可能であり、少数の支配的なパスではなく、多くの弱く建設的なパスを示しています。 ECC Attack Efficiency: Valid vs Invalid b above (Qwork のフルコード) は、可逆 b (キーリカバリーに便利) と non-invertible b (役に立たない) のサンプルの合計カウントを示しています。結果の半分以上は、無効な b 値 (gcd(b, 32) != 1) で無駄になります。6 ビット ブレークの次のデザインでは、有効な b ドメインで Oracle マスキングまたは選択後フィルタリングを使用できます。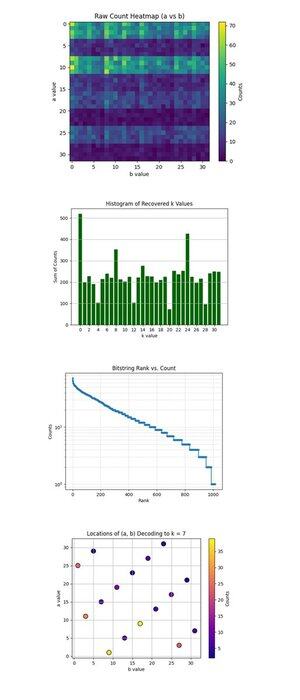 ヒートマップ: (a, b) と上記の可逆 b (mod 32) (Qwork のフルコード) は、b が k を回復するために必要な条件である可逆モジュロ 32 である (a, b) ペアのみに焦点を当てています。これは、量子干渉が 1024 ポイント空間内のどこに集中しているかを示しています。高強度領域は好ましい干渉経路を明らかにし、量子状態が不均一に進化したことを示唆しており、モジュラー乗算の下で特定の軌道が有利に働く可能性があります。これにより、一部の地域では、有効な候補を分離するのに十分な強度の信号コヒーレンスが確認されています。 上記の Phase Ridge Angles の分布 (Qwork のフルコード) は、平面内の (-a, b) ベクトル (モジュロ π) によって形成される角度をビン化しており、これは QFT 空間の位相リッジにほぼ対応しています。ヒストグラムのピークは、u + kv ≡ 0 の形式の強いアライメント、共振を示しており、完全な状態空間が広大であるにもかかわらず、回路が k を干渉パターンに正常にエンコードしたことを意味します。複数の支配的な角度は、隠れたシフトの高調波が存在することを示唆しています。 上記の a + 7b mod 32 の残基マップ(Qwork のフルコード)は、特定のターゲットキー k = 7 の出力残基を (a, b) 空間全体で視覚化します。ここでの一貫したバンドまたは対称性は、干渉が有効な解をどの程度増幅したかを示します (この値は 0 に等しい場合)。1024 格子のどの領域が a + 7b ≡ 0 に対応するかを観察でき、オラクルの構造がキーのインプリンティングに成功したことを検証できます。 ノイズ:上記の固定aのb間のカウントの分散(Qworkのフルコード)は、bを変化させるときに、各固定aの出力カウントがどれほどノイズが多いか安定しているかを示しています。分散が大きいということは、一部のb値が強い増幅につながり、他の値はそうではないということを意味し、そのa行の回路感度またはバックエンドノイズを意味します。滑らかな領域は量子コヒーレンスを意味し、スパイクはオラクル評価中のデコヒーレンスまたはエラー伝播を指す場合があります。 最終的に、この実験では、IBMの133量子ビット量子プロセッサ上で実行されるショアのアルゴリズムを使用して5ビットの楕円曲線キーを解読することに成功し、以前の4ビットの結果を大幅に大きな干渉空間(32x32 = 1024結果)に拡張しました。この回路は、秘密のスカラーkを参照せずにZ₃₂上のオラクルを符号化し、モジュラー群演算を利用してスカラーを位相干渉に絡め込みました。67,000層以上の深さの量子回路は、極端な回路深度にもかかわらず有効な干渉パターンを生成し、古典的な後処理では、上位100の可逆性(a、b)結果でk = 7が明らかになりました。この実験では、可視化を通じて、斜めのリッジ構造、可逆性マスク、干渉リッジの調和的な整列を確認し、量子コヒーレンスが正しいモジュラー関係を増幅するのに十分な強さを維持していることを検証しました。これは、ショアのアルゴリズムが深い回路レジームの下でスケーリングされ続け、ビット長が増加するにつれて辞書ベースの鍵回復戦略(上位100の列挙)が引き続き実行可能であり、ノイズの多い現実世界の条件下でも明確な量子的優位性を示していることを立証しています。 コード # メイン回路 # インポート インポートログ、JSON から Math Import GCD numpyをnpとしてインポート から qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile qiskit.circuit.libraryからユニタリーゲート、QFTをインポートします qiskit_ibm_runtimeからインポートQiskitRuntimeService、SamplerV2 Pandas を PD としてインポート # イブンク トークン = "YOUR_IBMQ_API_KEY" インスタンス = "YOUR_IBMQ_CRN" バックエンド = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/ダウンロード/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" ショット数 = 16384 # トイカーブパラメータ(E(F_p)の次数32サブグループ) 順序= 32 # |E(F_p)|= 32 P_IDX = 1 # 発電機 P -> インデックス 1 Q_IDX = 23 # 公共の点 Q = kP、ここでは k = 7 の "23 mod 32" # ロギングヘルパー logging.basicConfig(レベル = ログ記録 .INFO, format="%(asctime)s |%(レベル名)s |%(メッセージ)s") log = logging.getLogger(__name__) # キャリブレーションベースの量子ビットピック def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() 勝者 = ( df.sort_values(["√x (sx) エラー", "T1 (us)", "T2 (us)"], ascending=[真, 偽, 偽]) ["量子ビット"].head(n).tolist() ) log .info("最高の物理量子ビット: %s", 勝者) リターンウィナー N_Q = 5 N_Q_TOTAL = N_Q * 3 # a、b、ポイント 物理 = best_qubits(CAL_CSV, N_Q_TOTAL) # 再利用可能なゲートとしての定数加算器モジュロ32 def add_const_mod32_gate(c: int) -> UnitaryGate: """|x⟩ ↦ |x+c (mod 32)⟩をマップする5量子ビットゲートを返します。""" マット = np.zeros((32, 32)) 範囲(32)のxの場合: mat[(x + c) % 32, x] = 1 ユニタリーゲート(mat, label=f"+{c}") を返す 追加 = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, 定数): """Apply |x⟩ → |x+constant (mod 32)⟩ 1量子ビットで制御されます。""" qc.append(ADDERS[定数].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (インデックス演算 mod 32) def ecdlp_oracle(QC、a_reg、b_reg、point_reg): 範囲(N_Q)内のiの場合: 定数 = (P_IDX * (1 << i)) % 次数 定数の場合: controlled_add(QC、a_reg[i]、point_reg、定数) 範囲(N_Q)内のiの場合: constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # 完全な Shor 回路を構築 def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc、a、b、p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) QCを返す # IBM ランタイムの実行 サービス = QiskitRuntimeService(channel="ibm_cloud", token=トークン、 instance=インスタンス) バックエンド = service.backend(バックエンド) log .info("バックエンド → %s", バックエンド .name) qc_raw = shor_ecdlp_circuit() trans = トランスパイル(qc_raw, backend=バックエンド、 initial_layout=物理的、 optimization_level=3) log .info("回路の深さ %d, ゲート数 %s", trans.depth(), trans.count_ops()) サンプラー = SamplerV2(mode=バックエンド) ジョブ = サンプラー .run([trans], shots=SHOTS) result = job.result() # 従来のポストプロセッシング creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): 戻り値 int(bs[::-1], 2) カウント = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v counts_raw.items()} の k, v の場合 top = sorted(counts.items(), key=ラムダ kv: kv[1], reverse=True) # 達成基準。k = 7 の上位 100 の可逆行を確認します top_invertibles = [] (a_val, b_val) の場合、一番上の freq: gcd(b_val, ORDER) != 1 の場合: 続ける inv_b = pow(b_val, -1, 順序) k_candidate = (-a_val * inv_b) % 注文 top_invertibles.append(((a_val, b_val), k_candidate, freq)) len(top_invertibles) == 100 の場合: 壊す # 成功の確認と印刷結果 found_k7 = any(k == 7 for (_, k, _) in top_invertibles) found_k7の場合: print("\n成功 — k = 7 が上位 100 件の結果で見つかりました\n") 然も無くば： print("\n警告 - k = 7 トップ 100 の結果に見つかりません\n") print("上位100の可逆(a、b)ペアと回復したk:") (a, b), k の場合、top_invertiblesでカウントします。 tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # 生データを保存する アウト = { "実験": "ECDLP_32pts_Shors", "backend": バックエンド .name, 「physical_qubits」:物理的、 "shots": ショット, 「カウント」:counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" open(JSON_PATH, "w") を fp として使う場合: json.dump(出力、fp、インデント= 4) log .info("%s →結果を保存しました", JSON_PATH) # 終了 Qwork上の実行データを使用したすべての視覚化の完全なコード。