Rompere una chiave Ellittica a 5 bit con un computer quantistico a 133 qubit ⚛️ Questo esperimento rompe una chiave crittografica ellittica a 5 bit utilizzando l'algoritmo di Shor. Eseguito su @IBM's 133-qubit ibm_torino con @qiskit, un circuito a 15 qubit, composto da 10 qubit logici e 5 ancilla, interferisce su ℤ₃₂ per estrarre il valore scalare segreto k dalla relazione della chiave pubblica Q = kP, senza mai codificare k direttamente nell'oracolo. Da 16.384 scatti, l'interferenza quantistica rivela una cresta diagonale nello spazio di esito QFT 32x32. Il circuito quantistico, profondo oltre 67.000 strati, ha prodotto schemi di interferenza validi nonostante l'estrema profondità del circuito, e l'elaborazione post-classica ha rivelato k = 7 nei primi 100 risultati invertibili (a, b). Analisi del Codice 1. Codifica di Gruppo Limitare l'attenzione al sottogruppo di ordine 32 ⟨𝑃⟩ di una curva ellittica su 𝐹_p. Mappare i punti a interi: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. La legge di gruppo diventa somma modulare: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Questo esperimento utilizza una curva ellittica su F_p​ con un sottogruppo ciclico di ordine 32, mappando P -> 1 e Q = 7P -> 23 in ℤ₃₂​. Il codice assume la moltiplicazione scalare precomputata, astrando via le coordinate esplicite. 2. Registri Quantistici Registro a: cinque qubit per l'esponente 𝑎 ∈ {0, …, 31}. Registro b: cinque qubit per 𝑏 ∈ {0, …, 31}. Registro p: cinque qubit inizializzati a ∣0⟩ per contenere l'indice del punto. Registro classico c: un registro a 10 bit per registrare i valori misurati di a e b. 3. Preparazione della Sovrapposizione Applicare Hadamard a ogni qubit in a e b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Costruzione dell'Oracolo U_f L'obiettivo è una mappa reversibile: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Aggiungere aP: per ogni bit a_i (peso 2^𝑖), aggiungere (2^𝑖 P) mod 32 Aggiungere bQ: calcolare (2^𝑖 𝑄) mod 32, quindi aggiungere controllato su 𝑏_𝑖. Questi utilizzano porte di permutazione controllate a 5 qubit. Tutte le costanti sono derivate dal generatore P della curva ellittica e dal punto pubblico Q. Nessuna porta fa mai riferimento direttamente al segreto k. 5. Stato Globale dopo l'Oracolo Lo stato evolve in: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, dove f(a, b) = a + kb (mod32). a, b 6. Isolare il Registro del Punto L'algoritmo ha bisogno solo della relazione di fase in 𝑎, 𝑏. Una barriera isola p. 7. Trasformata di Fourier Quantistica (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Schema di Interferenza L'ampiezza congiunta per osservare (u, v) è: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), che forma una cresta diagonale nella griglia di esito 32x32. 9. Misurazione Misurare tutti e dieci i qubit logici. I risultati si concentrano su 32 coppie distinte che soddisfano u + kv ≡ 0 (mod 32). 10. Elaborazione Post-Classica Le stringhe di bit vengono invertite e analizzate in coppie (a, b). Mantenere solo le righe in cui gcd⁡(b, 32) = 1, assicurando che b sia invertibile. La chiave candidata viene calcolata come: k = (-a) b^(-1) mod 32 Lo script quindi: Estrae i primi 100 risultati invertibili (a, b) con il conteggio più alto. Calcola k per ciascuno. Stampa ogni coppia (a, b), k recuperato e conteggio. Dichiara successo se k = 7 appare nei primi 100. 11. Verifica e Archiviazione Il corretto scalare k = 7 è confermato se appare nei primi 100 risultati invertibili. Tutti i conteggi di stringhe di bit grezze, layout dei qubit e metadati vengono salvati in JSON per ulteriori visualizzazioni e analisi. Risultati 2025-06-25 19:41:29,294 | INFO | Profondità del circuito 67428, conteggi delle porte OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Inviando lavoro utilizzando opzioni {'options': {}, 'version': 2, 'support_qiskit': True} SUCCESS — k = 7 trovato nei primi 100 risultati Primi 100 coppie invertibili (a, b) e k recuperato: (a= 8, b=11) → k = 8 (conteggio = 63) (a=12, b= 9) → k = 20 (conteggio = 58) (a= 0, b= 3) → k = 0 (conteggio = 54) (a= 1, b= 9) → k = 7 (conteggio = 54) <<< (a=28, b= 1) → k = 4 (conteggio = 53) (a= 0, b=11) → k = 0 (conteggio = 53) (a= 8, b= 9) → k = 24 (conteggio = 53) (a= 8, b= 3) → k = 8 (conteggio = 53) ... (a=11, b= 3) → k = 7 (conteggio = 41) <<< ... (a=25, b= 1) → k = 7 (conteggio = 32) <<< Questa esecuzione ha recuperato con successo il valore scalare segreto k = 7 utilizzando una chiave ECC a 5 bit (sottogruppo di ordine 32), estendendo il mio precedente attacco a 4 bit a uno spazio con 1024 possibili combinazioni (a, b) e φ(32) = 16 valori b invertibili. k = 7 appare tre volte nei primi 100: (a = 1, b = 9) -> k = 7 con 54 conteggi (a = 11, b = 3) -> k = 7 con 41 conteggi (a =25, b = 1) -> k = 7 con 32 conteggi Questi sono stati ad alta frequenza, rendendoli credibili vettori di attacco sotto l'elaborazione post-classica. I conteggi mostrano concentrazione attorno a relazioni modulari strutturate: a + kb ≡ 0 mod 32. Queste appaiono come creste diagonali nello spazio di misurazione 32x32. Diversi valori di k ricorrono spesso (k = 0, 24, 28), mostrando la sovrapposizione probabilistica intrinseca all'interferenza quantistica, alcuni di questi sono falsi positivi da rumore o aliasing con altre equivalenze modulari. La profondità del circuito era di 67.428, con un totale di 106.455 porte, riflettendo una routine quantistica grande e complessa per l'aritmetica dell'indice modulare controllato. Questo potrebbe essere il maggior numero di porte che ho utilizzato in un circuito. Conteggi delle porte per il circuito: sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Totale porte: 106455 Profondità: 67428 Larghezza: 133 qubit | 10 clbits Questo esperimento ha impiegato 54 secondi per completarsi su 'ibm_torino'. Il profilo di rumore è non uniforme ma decrescente, il che significa che il sistema quantistico ha probabilmente risolto armoniche dominanti nell'interferenza ma ha sfocato strutture più fini. La coda della distribuzione contiene ancora candidati validi k = 7, questo supporta attacchi quantistici in stile dizionario dove le scansioni dei risultati top-N (N = 100) sono sufficienti per recuperare la chiave. 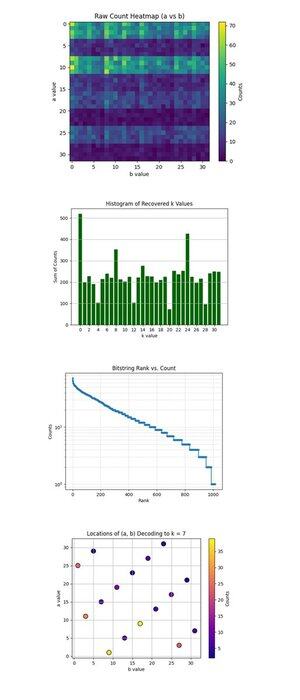La Mappa di Calore dei Conteggi Grezzi (a vs b) sopra (codice completo su Qwork) mostra una griglia 32x32 che rappresenta i conteggi osservati per ogni coppia (a, b) dopo aver eseguito il circuito di Shor. La mappa di calore mostra una distribuzione a bande e irregolare, indicando creste di interferenza, non rumore. Alcune righe (valori a) hanno una concentrazione visibilmente più alta, suggerendo interferenza costruttiva lungo specifiche soluzioni a + kb ≡ 0 mod 32. L'Istogramma dei Valori k Recuperati sopra (codice completo su Qwork) aggrega i conteggi totali per ogni chiave scalare recuperata k ∈ Z₃₂, derivata tramite k = −ab^(−1) mod 32. Un enorme picco a k = 0 e un altro attorno a k = 24 sono dominanti. La chiave corretta k = 7 non è la più alta, ma è ben rappresentata (~54 + 41 + 32 = 127 conteggi attraverso più coppie (a, b)). Questo mostra che gli hacker possono attaccare un numero maggiore di risultati in stile dizionario. Il Grafico di Rango delle Stringhe di Bit vs Conteggio (Scala Logaritmica) sopra (codice completo su Qwork) mostra un grafico di rango simile a Zipf di tutte le stringhe di bit per conteggio decrescente. L'asse y in scala logaritmica mostra una coda esponenziale, la maggior parte dei risultati si verifica <10 volte. La testa (circa 50) delle stringhe di bit ha una probabilità notevolmente più alta, indicando picchi di interferenza costruttiva. Potresti costruire un attacco quantistico euristico in stile dizionario che raccoglie solo le prime N stringhe di bit con un ritorno esponenziale sul segnale. Questo convalida che la struttura segnale-rumore quantistica è ancora intatta anche con circuiti più lunghi (67428 di profondità). Le Posizioni di Decodifica (a, b) a k = 7 sopra (codice completo su Qwork) mostrano che ogni punto è una coppia (a, b) che ha decodificato a k = 7. L'intensità del colore è pari al numero di volte in cui questa coppia è apparsa. Il grafico mostra una distribuzione relativamente uniforme attraverso (a, b), ma con picchi locali a (1, 9), (11, 3), (25, 1). Diverse combinazioni (a, b) convergono a k = 7 con molteplicità non uniforme. Da un punto di vista crittanalitico, questo convalida che l'algoritmo di Shor può rompere affidabilmente le chiavi ECC anche quando il corretto k non è il primo risultato. La Maschera di Invertibilità per il Registro b sopra (codice completo su Qwork) mostra un grafico a barre dei conteggi per ogni b ∈ {0, …, 31} che sono coprimi con 32 (gcd⁡(b, 32) = 1, solo questi sono invertibili modulo 32 e utili per recuperare k tramite: k = (−a)b^(−1) mod 32. I b invertibili sono ben popolati, mostrando che il circuito ha prodotto candidati recuperabili. Maggiore uniformità qui aumenterebbe la potenza di elaborazione post-classica, idealmente, questi sarebbero piatti. La Mappa di Frequenza dell'Inverso Modulare: b vs b^(−1) mod 32 sopra (codice completo su Qwork) mostra una mappa di calore di quanto spesso ogni b invertibile si mappa al corrispondente inverso modulare b^(−1) mod 32, pesata dai conteggi dei risultati. La maggior parte dei punti cade su una linea bijettiva pulita, ogni b si mappa pulitamente a un unico b^(−1), confermando la correttezza dell'inversione modulare. Le regioni più luminose (vicino all'angolo in basso a sinistra o in alto a destra) mostrano b favoriti dal campionamento quantistico. Nessun rumore o raggruppamento fuori diagonale, buon segno di una struttura modulare pulita preservata. La Mappa a + 7b mod 32 sopra (codice completo su Qwork) assume k = 7 e traccia il valore di (a + 7b) mod 32 attraverso tutti i risultati. La distribuzione è quasi uniforme. Questo suggerisce che non ci sia una cresta di interferenza netta come nel caso a 4 bit. Perché? Il circuito a 5 bit (con 10 qubit logici) distribuisce l'ampiezza più sottile attraverso 1024 risultati, riducendo il contrasto. Eppure la chiave corretta era ancora recuperabile, indicando molti percorsi debolmente costruttivi, piuttosto che pochi dominanti. L'Efficienza dell'Attacco ECC: b Validi vs Non Validi sopra (codice completo su Qwork) mostra conteggi totali da campioni con b invertibili (utili per il recupero della chiave) vs. b non invertibili (inutili). Oltre la metà dei risultati sono sprecati su valori b non validi (gcd⁡(b, 32) != 1). Il prossimo design per una rottura a 6 bit potrebbe utilizzare mascheramento oracolare o filtraggio post-selezione su domini b validi. 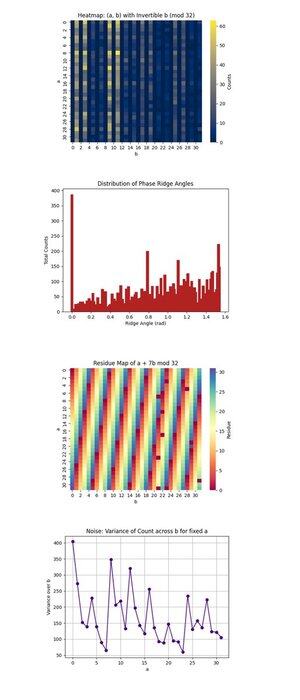La Mappa di Calore: (a, b) con b Invertibile (mod 32) sopra (codice completo su Qwork) si concentra solo su coppie (a, b) dove b è invertibile modulo 32, una condizione necessaria per recuperare k. Mostra dove l'interferenza quantistica si concentra all'interno dello spazio di 1024 punti. Le regioni ad alta intensità rivelano percorsi di interferenza preferiti, suggerendo che lo stato quantistico è evoluto in modo non uniforme, favorendo possibilmente certe orbite sotto la moltiplicazione modulare. Conferma una coerenza del segnale sufficientemente forte in alcune regioni per isolare candidati validi. La Distribuzione degli Angoli della Cresta di Fase sopra (codice completo su Qwork) raggruppa gli angoli formati dai vettori (-a, b) nel piano, modulo π, che corrispondono grossolanamente alle creste di fase nello spazio QFT. I picchi nell'istogramma indicano forti allineamenti, risonanze, della forma u + kv ≡ 0, il che significa che il circuito ha codificato con successo k nel modello di interferenza anche se l'intero spazio di stato è vasto. Gli angoli dominanti multipli suggeriscono che sono presenti armoniche dello spostamento nascosto. La Mappa dei Residui di a + 7b mod 32 sopra (codice completo su Qwork) visualizza il residuo di output per la chiave target specifica k = 7, attraverso l'intero spazio (a, b). Qualsiasi banda o simmetria consistente qui indica quanto bene l'interferenza ha amplificato le soluzioni valide (dove questo valore è uguale a 0). Puoi osservare quali regioni della griglia 1024 corrispondono a a + 7b ≡ 0, convalidando che la struttura dell'oracolo ha portato a un'impronta di chiave di successo. Il Rumore: Varianza del Conteggio attraverso b per a fisso sopra (codice completo su Qwork) mostra quanto siano rumorosi o stabili i conteggi di output per ciascun a fisso mentre variamo b. Alta varianza significa che alcuni valori b portano a forti amplificazioni mentre altri no, implicando sensibilità del circuito o rumore di backend per quella riga a. Le regioni lisce implicano coerenza quantistica, mentre i picchi possono indicare decoerenza o propagazione di errori durante la valutazione dell'oracolo. Alla fine, questo esperimento ha rotto con successo una chiave ellittica a 5 bit utilizzando l'algoritmo di Shor eseguito sul processore quantistico a 133 qubit di IBM, estendendo il precedente risultato a 4 bit in uno spazio di interferenza significativamente più grande (32x32 = 1024 risultati). Questo circuito ha codificato l'oracolo su ℤ₃₂ senza mai fare riferimento al valore scalare segreto k, e ha sfruttato l'aritmetica del gruppo modulare per intrecciare lo scalare nell'interferenza di fase. Il circuito quantistico, profondo oltre 67.000 strati, ha prodotto schemi di interferenza validi nonostante l'estrema profondità del circuito, e l'elaborazione post-classica ha rivelato k = 7 nei primi 100 risultati invertibili (a, b). Attraverso visualizzazioni, questo esperimento ha confermato strutture a cresta diagonale, maschere di invertibilità e allineamento armonico delle creste di interferenza, convalidando che la coerenza quantistica è rimasta sufficientemente forte da amplificare la corretta relazione modulare. Questo stabilisce che l'algoritmo di Shor continua a scalare sotto regimi di circuito più profondi e che le strategie di recupero della chiave basate su dizionario (enumerazione dei primi 100) rimangono praticabili man mano che aumenta la lunghezza dei bit, mostrando un chiaro vantaggio quantistico anche in condizioni reali rumorose. Codice # Circuito principale # Importazioni import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Parametri della curva giocattolo (sottogruppo di ordine 32 di E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Generatore P -> indice 1 Q_IDX = 23 # Punto pubblico Q = kP, qui “23 mod 32” per k = 7 # Helper di logging logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Selezione dei qubit basata sulla calibrazione def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Migliori qubit fisici: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punto PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Sommatore costante modulo 32 come porta riutilizzabile def add_const_mod32_gate(c: int) -> UnitaryGate: """Restituisce una porta a 5 qubit che mappa |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Applica |x⟩ → |x+constant (mod 32)⟩ controllato da un qubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oracolo U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (aritmetica degli indici mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Costruire l'intero circuito di Shor def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Esecuzione del runtime IBM service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Profondità del circuito %d, conteggi delle porte %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Elaborazione post-classica creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Criteri di successo. Controlla le prime 100 righe invertibili per k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Controlla il successo e stampa i risultati found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nSUCCESS — k = 7 trovato nei primi 100 risultati\n") else: print("\nWARNING — k = 7 NON trovato nei primi 100 risultati\n") print("Primi 100 coppie invertibili (a, b) e k recuperato:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (conteggio = {count}){tag}") # Salva i dati grezzi out = { "esperimento": "ECDLP_32pts_Shors", "backend": backend .name, "qubit_fisici": PHYSICAL, "scatti": SHOTS, "conteggi": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Risultati salvati → %s", JSON_PATH) # Fine Codice completo per tutte le visualizzazioni utilizzando i dati di esecuzione su Qwork.