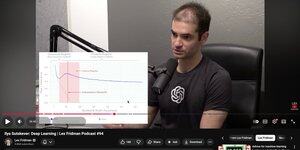
Handlowanie między biasem a wariancją ma brakujący szczegół! Niewielu inżynierów ML o tym wie. Rozważ dopasowanie modelu regresji wielomianowej do jakiegoś sztucznego zbioru danych, powiedzmy, y=sin(x) + szum. Jak pokazano na pierwszym wykresie w obrazie, gdy zwiększamy stopień (m): - Strata na zbiorze treningowym spadnie do zera. - Strata na zbiorze testowym (lub walidacyjnym) będzie malała, a następnie wzrośnie. Ale zauważ, co się dzieje, gdy nadal zwiększamy stopień (m): ↳ Strata testowa ponownie maleje (pokazane na drugim wykresie) Nazywa się to „fenomenem podwójnego spadku” i jest powszechnie obserwowane w modelach głębokiego uczenia. Jest to sprzeczne z intuicją, ponieważ pokazuje, że zwiększenie złożoności modelu może poprawić wydajność generalizacji. Z tego, co mi wiadomo, to wciąż otwarte pytanie. Nie jest całkowicie jasne, dlaczego sieci neuronowe wykazują takie zachowanie. Istnieją pewne teorie dotyczące regularyzacji, jednak, takie jak ta: Może być tak, że model stosuje pewnego rodzaju implicitną regularyzację. W rezultacie może precyzyjnie skupić się na odpowiedniej liczbie parametrów dla generalizacji. W rzeczywistości możesz to sam spróbować: - Stwórz mały sztuczny zbiór danych o rozmiarze n. - Wytrenuj regresję wielomianową o stopniu m, zaczynając od 1 do wartości większej niż n. - Narysuj stratę testową i stratę treningową dla każdego m. 👉 A teraz do Ciebie: Czy słyszałeś wcześniej o podwójnym spadku?

Oto dokładny znacznik czasu, w którym Ilya Sutskever o tym mówi w podcaście Lexa Fridmana: