Bryte en 5-biters elliptisk kurvenøkkel med en 133-qubit kvantedatamaskin ⚛️ Dette eksperimentet bryter en 5-bits elliptisk kurve kryptografisk nøkkel ved hjelp av Shors algoritme. Utført på @IBM s 133-qubit ibm_torino med @qiskit, en 15-qubit-krets, bestående av 10 logiske qubits og 5 ancilla, interfererer over Z₃₂ for å trekke ut den hemmelige skalaren k fra den offentlige nøkkelrelasjonen Q = kP, uten noen gang å kode k direkte inn i orakelet. Fra 16 384 bilder avslører kvanteinterferensen en diagonal rygg i 32x32 QFT-utfallsrommet. Kvantekretsen, over 67 000 lag dyp, produserte gyldige interferensmønstre til tross for ekstrem kretsdybde, og klassisk etterbehandling avslørte k = 7 i de 100 beste invertible (a, b) resultatene. Gjennomgang av kode 1. Koding av grupper Begrens oppmerksomheten til orden-32-undergruppen ⟨P⟩ av en elliptisk kurve over F_p. Kart peker på heltall: 0P -> 0, 1P -> 1, ..., 31P -> 31. Grupperett blir modulært tillegg: (xP) + (yP) = ((x + y) mod 32))P. Dette eksperimentet bruker en elliptisk kurve over F_p med en syklisk undergruppe av orden 32, og kartlegger P -> 1 og Q = 7P -> 23 i Z₃₂. Koden forutsetter forhåndsberegnet skalarmultiplikasjon, og abstraherer bort eksplisitte koordinater. 2. Kvanteregistre Registrer a: fem kvantebiter for eksponenten a ∈ {0, ..., 31}. Registrer b: fem qubits for b ∈ {0, ..., 31}. Registrer p: fem kvantebiter initialisert til ∣0⟩ for å holde poengindeksen. Klassisk register c: et 10-bits register for å registrere de målte verdiene til a og b. 3. Forberedelse av superposisjon Påfør Hadamards på hver qubit i a og b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Orakelkonstruksjon U_f Goal er et reversibelt kart: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Legg til aP: for hver bit a_i (vekt 2^i), legg til (2^i P) mod 32 Legg til bQ: compute (2^i Q) mod 32, og legg deretter til kontrollert på b_i. Disse bruker 5-qubit-kontrollerte permutasjonsporter. Alle konstanter er avledet fra den elliptiske kurvens generator P og det offentlige punktet Q. Ingen port refererer noen gang direkte til hemmeligheten k. 5. Global stat etter Oracle Staten utvikler seg til: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, hvor f(a, b) = a + kb (mod32). a, b 6. Isoler punktregister Algoritmen trenger bare faserelasjonen i a, b. En barriere isolerer s. 7. Kvantefouriertransformasjon (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Interferens mønster Felles amplitude for observasjon (u, v) er: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), som danner en diagonal rygg i 32x32 utfallsrutenettet. 9. Måling Mål alle ti logiske kvantebitene. Utfallene konsentrerer seg om de 32 distinkte parene som tilfredsstiller u + kv ≡ 0 (mod 32). 10. Klassisk etterbehandling Bitstrenger er endian-flippet og analysert i (a, b) par. Behold bare rader der gcd(b, 32) = 1, og sørg for at b er inverterbar. Kandidatnøkkelen beregnes som: k = (-a) b^(-1) mod 32 Manuset så: Trekker ut de 100 beste resultatene med høyest antall inverterbare (a, b). Beregner k for hver. Skriver ut hvert (a, b) par, gjenopprettet k og antall. Erklærer suksess hvis k = 7 vises blant de 100 beste. 11. Verifisering og lagring Riktig skalar k = 7 bekreftes hvis den vises i de 100 beste inverterbare resultatene. Alle rå bitstrengantall, qubit-oppsett og metadata lagres i JSON for videre visualisering og analyse. Resultater 25.06.2025 19:41:29.294 | INFORMASJON | Kretsdybde 67428, porttellinger OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Sende inn jobb ved hjelp av alternativer {'options': {}, 'version': 2, 'support_qiskit': True} SUKSESS — k = 7 funnet i topp 100 resultater Topp 100 invertible (a, b) par og gjenopprettet k: (a= 8, b=11) → k = 8 (antall = 63) (a=12, b= 9) → k = 20 (antall = 58) (a= 0, b= 3) → k = 0 (antall = 54) (a= 1, b= 9) → k = 7 (antall = 54) <<< (a=28, b= 1) → k = 4 (antall = 53) (a= 0, b=11) → k = 0 (antall = 53) (a= 8, b= 9) → k = 24 (antall = 53) (a= 8, b= 3) → k = 8 (antall = 53) ... (a=11, b= 3) → k = 7 (antall = 41) <<< ... (a=25, b= 1) → k = 7 (antall = 32) <<< Denne kjøringen hentet den hemmelige skalaren k = 7 ved hjelp av en 5-bits ECC-nøkkel (ordre-32 undergruppe), og utvidet mitt forrige 4-bits angrep til et mellomrom med 1024 mulige (a, b) kombinasjoner og φ(32) = 16 inverterbare b-verdier. k = 7 vises tre ganger i topp 100: (a = 1, b = 9) -> k = 7 med 54 tellinger (a = 11, b = 3) -> k = 7 med 41 tellinger (a = 25, b = 1) -> k = 7 med 32 tellinger Dette er høyfrekvente tilstander, noe som gjør dem til troverdige angrepsvektorer under klassisk etterbehandling. Tellingene viser konsentrasjon rundt strukturerte modulære relasjoner: a + kb ≡ 0 mod 32. Disse vises som diagonale rygger i 32x32 målerommet. Flere k-verdier gjentar seg ofte (k = 0, 24, 28), og viser den probabilistiske overlappingen iboende kvanteinterferens, noen av disse er falske positiver fra støy eller aliasing med andre modulære ekvivalenser. Kretsdybden var 67 428, med totalt 106 455 porter, noe som gjenspeiler en stor, kompleks kvanterutine for kontrollert modulær indeksaritmetikk. Dette kan være det største antallet porter jeg har brukt i en krets. Porttellinger for kretsen: Sx: 56613 cz: 34319 RZ: 15355 x: 157 Mål: 10 barriere: 1 Totalt antall porter: 106455 Dybde: 67428 Bredde: 133 qubits | 10 klbiter Dette eksperimentet tok 54 sekunder å fullføre på 'ibm_torino'. Støyprofilen er ujevn, men avtagende, noe som betyr at kvantesystemet sannsynligvis løste dominerende harmoniske i interferensen, men visket ut finere strukturer. Distribusjonshalen inneholder fortsatt gyldige k = 7 kandidater, dette støtter kvanteangrep i ordbokstil der topp-N-resultatskanninger (N = 100) er tilstrekkelig til å hente nøkkelen. 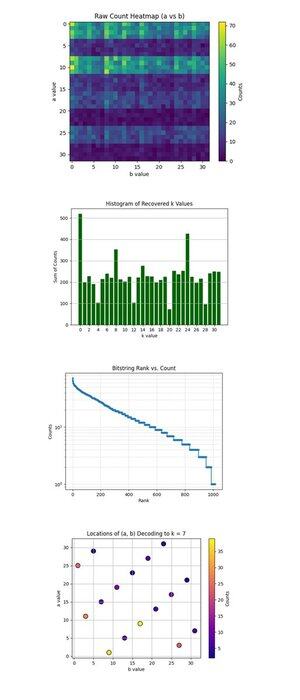Raw Count Heatmap (a vs b) ovenfor (full kode på Qwork) viser at et 32x32 rutenett representerer de observerte tellingene for hvert par (a, b) etter å ha kjørt Shors krets. Varmekartet viser en båndet og ujevn fordeling, som indikerer interferensrygger, ikke støy. Enkelte rader (a-verdier) har synlig høyere konsentrasjon, noe som tyder på konstruktiv interferens langs spesifikke a + kb ≡ 0 mod 32-løsninger. Histogrammet for gjenopprettede k-verdier ovenfor (full kode på Qwork) aggregerer det totale antallet for hver gjenopprettede skalarnøkkel k ∈ Z₃₂, avledet via k = −ab^(−1) mod 32. En stor pigg ved k = 0 og en annen rundt k = 24 er dominerende. Den riktige nøkkelen k = 7 er ikke den høyeste, men er godt representert (~54 + 41 + 32 = 127 tellinger på tvers av flere (a, b) par). Dette viser at hackere kan ordbokangrep en større mengde resultater. Bitstring Rank vs Count (Log-Scale) ovenfor (full kode på Qwork) viser et Zipf-lignende rangeringsplott av alle bitstrenger ved synkende antall. Y-aksen i log-skala viser en eksponentiell hale, de fleste utfall forekommer <10 ganger. Hodebitstrengene (topp ~50) har bratt høyere sannsynlighet, noe som indikerer konstruktive interferenstopper. Du kan bygge et kvanteheuristisk ordbokangrep som bare høster de øverste N-bitstrengene med eksponentiell avkastning på signal. Dette validerer at kvantesignal-til-støy-strukturen fortsatt er intakt selv med lengre kretser (67428 dybde). Plasseringen av (a, b) Dekoding til k = 7 ovenfor (full kode på Qwork) viser at hver prikk er et (a, b) par som dekodet til k = 7. Fargeintensitet tilsvarer antall ganger dette paret oppstod. Plottet viser en relativt jevn fordeling på tvers av (a, b), men med lokale topper på (1, 9), (11, 3), (25, 1). Flere (a, b) kombinasjoner konvergerer til k = 7 med ujevn multiplisitet. Fra et kryptoanalytisk synspunkt validerer dette at Shors algoritme pålitelig kan bryte ECC-nøkler selv når riktig k ikke er topp 1-resultatet. Invertibilitetsmasken for b-registeret ovenfor (full kode på Qwork) viser et søylediagram over tellinger for hver b ∈ {0, ..., 31} som er coprime med 32 (gcd(b, 32) = 1, bare disse er invertible modulo 32 og nyttige for å gjenopprette k via: k = (−a)b^(−1) mod 32. Invertible b-er er godt befolket, noe som viser at kretsen produserte gjenvinnbare kandidater. Mer ensartethet her ville øke etterbehandlingskraften, ideelt sett ville disse være flate. Modular Inverse Frequency Map: b vs b^(−1) mod 32 ovenfor (full kode på Qwork) viser et varmekart over hvor ofte hver invertible b tilordnes til hver tilsvarende modulære inverse b^(−1) mod 32, vektet etter resultatantall. De fleste punkter faller på en ren bijektiv linje, hver b kartlegger rent til en unik b^(−1), noe som bekrefter riktigheten av modulær inversjon. Lysere områder (nær nederst til venstre eller øverst til høyre) viser favoriserte b-er fra kvanteprøvetakingen. Ingen off-diagonal støy eller klynger, godt tegn på ren modulær struktur bevart. A + 7b mod 32-kartet ovenfor (full kode på Qwork) antar k = 7 og plotter verdien av (a + 7b) mod 32 på tvers av alle resultatene. Fordelingen er nesten jevn. Dette antyder ingen skarp interferensrygg som i 4-bits tilfellet. Hvorfor? 5-bits kretsen (med 10 logiske qubits) sprer amplitude tynnere over 1024 utfall, noe som reduserer kontrasten. Likevel var den riktige nøkkelen fortsatt gjenvinnbar, noe som indikerte mange svakt konstruktive veier, snarere enn noen få dominerende. ECC-angrepseffektiviteten: Gyldig vs ugyldig b ovenfor (full kode på Qwork) viser totalt antall fra prøver med inverterbar b (nyttig for nøkkelgjenoppretting) vs. ikke-inverterbar b (ubrukelig). Over halvparten av resultatene er bortkastet på ugyldige b-verdier (gcd(b, 32) != 1). Neste design for en 6-biters pause kan bruke orakelmaskering eller ettervalgsfiltrering på gyldige b-domener. 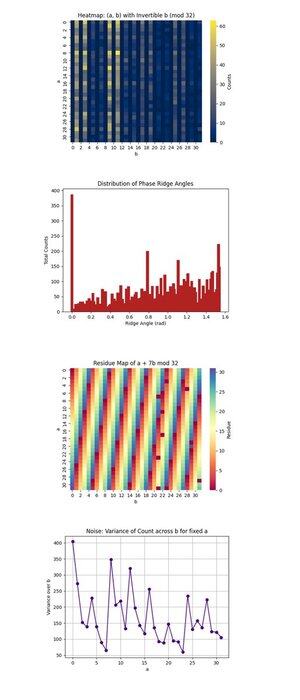Varmekartet: (a, b) med invertibel b (mod 32) ovenfor (full kode på Qwork) fokuserer bare på (a, b) par der b er invertibel modulo 32, en nødvendig betingelse for å gjenopprette k. Den viser hvor kvanteinterferens konsentrerer seg innenfor 1024-punktsrommet. Høyintensitetsregionene avslører foretrukne interferensbaner, noe som tyder på at kvantetilstanden utviklet seg ujevnt, muligens favoriserer visse baner under modulær multiplikasjon. Det bekrefter sterk nok signalsammenheng i noen regioner til å isolere gyldige kandidater. Fordelingen av faseryggvinkler ovenfor (full kode på Qwork) biner vinklene dannet av (-a, b) vektorer i planet, modulo π, som omtrent tilsvarer faserygger i QFT-rommet. Topper i histogrammet indikerer sterke justeringer, resonanser, av formen u + kv ≡ 0, noe som betyr at kretsen vellykket kodet k inn i interferensmønsteret selv om hele tilstandsrommet er stort. De mange dominante vinklene antyder at harmoniske av det skjulte skiftet er til stede. Restkartet til en + 7b mod 32 ovenfor (full kode på Qwork) visualiserer utgangsresten for den spesifikke målnøkkelen k = 7, over hele (a, b) rommet. Eventuelle konsistente bånd eller symmetrier her indikerer hvor godt interferensen amplifiserte gyldige løsninger (der denne verdien er lik 0). Du kan observere hvilke regioner i 1024-gitteret som tilsvarer en + 7b ≡ 0, noe som bekrefter at oraklets struktur førte til vellykket nøkkelpreging. Noise: Variance of Count over b for fixed a ovenfor (full kode på Qwork) viser hvor støyende eller stabile utgangstellingene var for hver faste a når vi varierer b. Høy varians betyr at noen b-verdier fører til sterk forsterkning mens andre ikke gjør det, noe som antyder kretsfølsomhet eller backend-støy for den a-raden. Glatte regioner innebærer kvantekoherens, mens pigger kan peke på dekoherens eller feilutbredelse under orakelevaluering. Til slutt brøt dette eksperimentet en 5-bits elliptisk kurvenøkkel ved å bruke Shors algoritme utført på IBMs 133-qubit kvanteprosessor, og utvidet det forrige 4-bits resultatet til et betydelig større interferensrom (32x32 = 1024 utfall). Denne kretsen kodet oraklet over Z₃₂ uten å referere til den hemmelige skalaren k, og utnyttet modulær gruppearitmetikk for å vikle skalaren inn i faseinterferens. Kvantekretsen, over 67 000 lag dyp, produserte gyldige interferensmønstre til tross for ekstrem kretsdybde, og klassisk etterbehandling avslørte k = 7 i de 100 beste invertible (a, b) resultatene. Gjennom visualiseringer bekreftet dette eksperimentet diagonale ryggstrukturer, invertibilitetsmasker og harmonisk justering av interferensrygger, og validerte at kvantekoherens forble sterk nok til å forsterke det riktige modulære forholdet. Dette fastslår at Shors algoritme fortsetter å skalere under dypere kretsregimer, og at ordbokbaserte nøkkelgjenopprettingsstrategier (topp 100-opptelling) forblir levedyktige etter hvert som bitlengden øker, og viser klare kvantefordeler selv under støyende forhold i den virkelige verden. Kode # Hovedkrets # Importer Importlogging, JSON Fra Math Import GCD Importere Numpy som NP fra qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile fra qiskit.circuit.library-import UnitaryGate, QFT fra qiskit_ibm_runtime importere QiskitRuntimeService, SamplerV2 Importer pandaer som PD # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" FOREKOMST = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Brukere/steventippeconnic/Nedlastinger/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SKUDD = 16384 # Lekekurveparametere (rekkefølge-32 undergruppe av E(F_p)) REKKEFØLGE = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> indeks 1 Q_IDX = 23 # Offentlig punkt Q = kP, her "23 mod 32" for k = 7 # Logger hjelper logging.basicConfig(nivå=logging .INFO, format="%(asctime)s | %(nivånavn)s | %(melding)s") log = logging.getLogger(__name__) # Kalibreringsbasert qubit-plukk def best_qubits(csv_path: str, n: int) -> liste[int]: df = pd .read_csv(csv_path) df.kolonner = df.kolonner.str.strip() vinnere = ( df.sort_values(["√x (sx) feil", "T1 (oss)", "T2 (oss)"], stigende=[Sann, Usann, Usann]) ["Qubit"].head(n).tolist() ) log .info("Beste fysiske qubits: %s", vinnere) Returnere vinnere N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punkt FYSISK = best_qubits(CAL_CSV, N_Q_TOTAL) # Konstant-adder modulo 32 som en gjenbrukbar port def add_const_mod32_gate(c: int) -> UnitaryGate: """Returner en 5-qubit-port som tilordner |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.nuller((32, 32)) For x i området (32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c i område(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, konstant): """Bruk |x⟩ → |x+konstant (mod 32)⟩ kontrollert av én kvantebit.""" qc.append(ADDERS[konstant].kontroll(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (indeksaritmetisk mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i i område (N_Q): konstant = (P_IDX * (1 << i)) % REKKEFØLGE hvis konstant: controlled_add(qc, a_reg[i], point_reg, konstant) for i i område (N_Q): konstant = (Q_IDX * (1 << i)) % ORDEN hvis konstant: controlled_add(qc, b_reg[i], point_reg, konstant) # Bygg hele Shor-kretsen def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=Usann), a) qc.append(QFT(N_Q, do_swaps=Usann), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) Returner QC # IBM Runtime kjøring service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, forekomst=FOREKOMST) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=FYSISK, optimization_level=3) log .info("Kretsdybde %d, porter teller %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(modus=backend) jobb = sampler .run([trans], shots=SHOTS) resultat = jobb.resultat() # Klassisk etterbehandling creg_name = trans.cregs[0].name counts_raw = resultat[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): returner int(bs[::-1], 2) teller = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v i counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Suksesskriterier. Sjekk de 100 øverste inverterbare radene for k = 7 top_invertibles = [] For (a_val, b_val), Freq øverst: hvis gcd(b_val, ORDRE) != 1: fortsette inv_b = pow(b_val, -1, ORDEN) k_candidate = (-a_val * inv_b) % BESTILLING top_invertibles.tillegg(((a_val, b_val), k_candidate, freq)) hvis len(top_invertibles) == 100: pause # Se etter suksess og utskriftsresultater found_k7 = noen(k == 7 for (_, k, _) i top_invertibles) Hvis found_k7: print("\nSUKSESS — k = 7 funnet i topp 100 resultater\n") ellers: print("\nADVARSEL — k = 7 IKKE funnet i topp 100 resultater\n") print("Topp 100 inverterbare (a, b) par og gjenopprettet k:") for (a, b), k, teller i top_invertibles: tag = " <<<" hvis k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Lagre rådata ut = { "eksperiment": "ECDLP_32pts_Shors", "backend": backend .name, "physical_qubits": FYSISK, «skudd»: SKUDD, «teller»: counts_raw } JSON_PATH = "/Brukere/steventippeconnic/Dokumenter/QC/Shors_ECC_5_Bit_Key_0.json" med open(JSON_PATH, "w") som fp: json.dump(ut, fp, innrykk=4) log .info("Resultater lagret → %s", JSON_PATH) # Slutt Full kode for alle visualiseringer ved hjelp av kjøredata på Qwork.